応力-ひずみ曲線とは
「応力-ひずみ曲線」と聞くと難しそうですが、モノづくりの設計開発においては、決して欠かせない重要なグラフです。このグラフを見れば多くの「その材質の特性」がわかります。
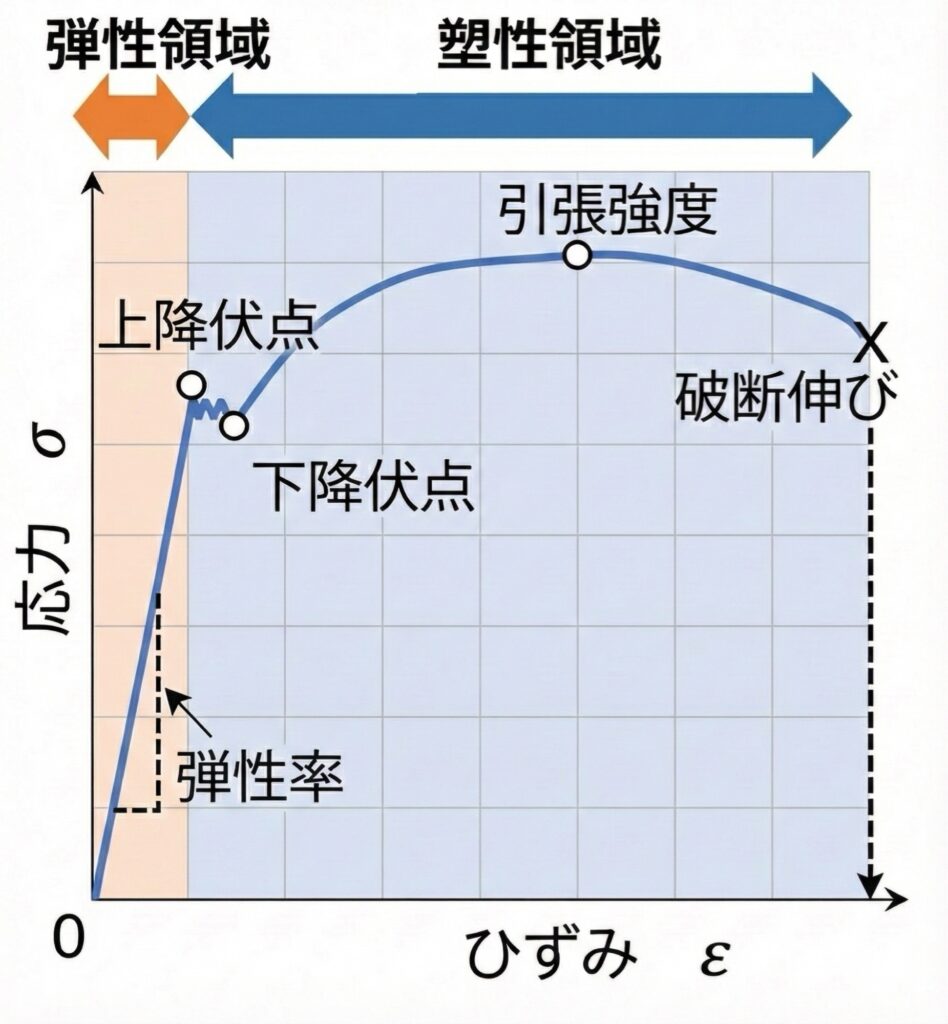
これはザックリひとことで言えば以下のようになります。
ものに対して”どれくらいの力”を加えたら、”どれくらい変形”し、”いつ壊れるのか”を表したグラフ
応力-ひずみ曲線を見れば、
- この材料はどのくらいまでなら耐えられるのか(弾性変形)
- どこから「元に戻れない変形(塑性変形)」が始まるのか
- 最後はどのくらいで壊れるのか(破断点)
といった材料の性質が、ひと目でわかるようになります。
応力(σ)とは
応力はひとことでいうと、
単位面積あたりに、どれくらいの強さで力がかかっているか
を表すものです。
「応力=荷重÷面積」の計算式で求められ、グラフでは上に行けば行くほど力が加わっていることを示します。
ひずみ(ε)とは
もう一方のひずみは、
元の長さに対して、どれくらい伸びた(縮んだ)かという“割合”
を表し、グラフでは右に行けば行くほどひずみが大きいことを示します。
例えば、
- 元の長さ:100mm
- 引っ張って伸びた量:1mm
という場合は、ひずみは「1÷100=0.01」、つまり「1%伸びた」ということになります。
ここでのポイントは、「何mm伸びたか」という絶対値ではなく、「何%伸びたか」という相対的な値であるということです。
それでは、今から応力-ひずみ曲線の基本構造をさらに見ていきましょう。
弾性率(ヤング率)
グラフの最初の直線部分の“傾き”は、「弾性率」または「ヤング率」と呼ばれます。
これは、
力を加えたとき、どれくらい変形するか、もしくは変形しないかを表す“硬さの指標”
となっており、
- 傾きが急:少しのひずみを出すのに大きな応力が必要→硬い材料
- 傾きが緩やか:同じ応力でもひずみが大きい→柔らかい材料
というように読み取ることができます。
弾性領域
弾性領域は、その材料に対して荷重をかけるのをやめた場合に、元に戻れる範囲を表します。
グラフでは、最初のほぼまっすぐな直線になっている部分(オレンジ色の部分)を指します。
この部分は、応力とひずみがきれいに比例していて、力を2倍にすると変形も2倍、といった関係になっており、
力を抜けば、元通りの形に戻る
のが特徴です。
降伏点・塑性領域
ここから荷重をどんどん強くしていき、ある境目を超えると、急激に応力が下がるポイントがあり、この点を「上降伏点」と呼びます。
上降伏点を超えると、もう力を抜いても元の形には戻れず、「塑性(そせい)領域」と呼ばれる領域に入ります。
そしてここから先は、ギザギザの波打ちのようなグラフを描きながら(応力を伸びるエネルギーに変換しながら)、「下降伏点」に到達します。
引張強さ
さらに引っ張り続けると、応力-ひずみ曲線はあるところで山の頂上のようなピークを迎えます。この一番高い点を「引張(ひっぱり)強さ」と言います。
その材料が耐えられる、最大限の強さ
を表しており、多くの金属材料で重要な指標として使われています。
破断点・破断伸び
その後、材料内部に細かいキズやくびれができ始め、最終的にプツッと切れます。
この切れた点は「破断点」と呼ばれ、破断するまでに元の長さから何%伸びたかを表すX軸(横軸)を、「破断伸び」と言います。
破断した瞬間に応力はゼロになるため、グラフとしては最後にストンと途切れるイメージになります。
靱性
応力-ひずみ曲線の下側の“面積”は「靱性(じんせい)」と呼ばれます。これは、
壊れるまでにどれくらいのエネルギーを吸収できるか
を表しています。
車のボディなどは、衝突時に人を守るために、つぶれながらもエネルギーを吸収してくれる方が望ましいため、ここの「靱性」が重要視されます。
「硬さ」だけでなく、「どう壊れるのか」も安全性に直結するのです。
なお、弾性領域内(上降伏点より左側)の三角形の面積は、「レジリエンス」または「弾性ひずみエネルギー」と呼ばれます。
まとめ
応力-ひずみ曲線が重要なのは、単に材料の「強さ」だけでなく、「どのように力を受け止め、どのように壊れるか」という材料の性質のすべてがそこに描かれているからです。
モノづくりでは、それらをふまえて設計開発をする必要があります。